Problem Formulation
This work solves the problem of defining an optimal control policy for a given autonomous system and environment setup. The system shall be steered to the goal state while minimizing the collision probability with dynamic obstacles. Furthermore, the state and input constraints must be satisfied, and the system dynamics can be nonlinear in the states.
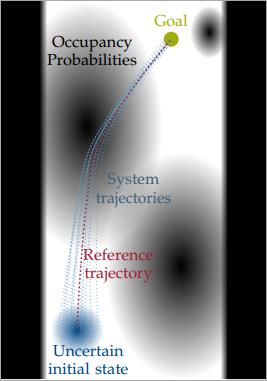
In contrast to classical motion planning problems, we consider an uncertain initial state following an arbitrary but known probability density function. During the execution of the control policy, the state can be measured and used for closed-loop control. However, because of limited computational power and the time constraints for real-time executability, the online computations of the controller have to be simple. Furthermore, we consider imperfect measurements due to sensor bias.
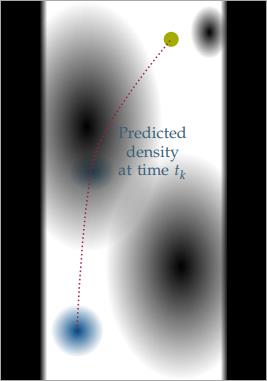
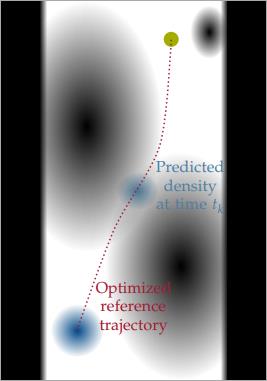
Additionally, probabilistic predictions for the evolution of the environment are given. Namely, we know for each position in the environment the probability of it being occupied by an obstacle at a certain point in time. The position of the vehicle at this time depends on the initial state and hence also follows a certain probability distribution. The overlap of this state distribution with the predicted obstacle positions yields the collision probability.
Thus, the algorithm should find a general control strategy which minimizes the cost function and satisfies the constraints for the uncertain initial states despite sensor errors. The motion planning problems are visualized in the figures below.
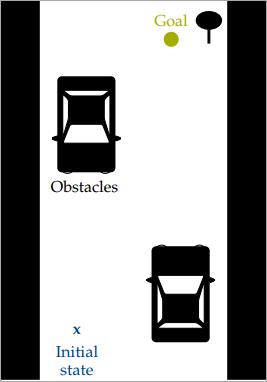
Classical motion planning problem: The initial state and the environment is considered as known.
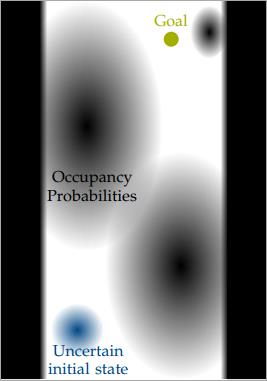
Motion planning problem considered in this work: The initial state is uncertain and given by an arbitrary probability distribution. The environment is uncertain and described by occupancy probabilities.