We consider the problem of designing distributed collision-avoidance multi-agent control in large-scale environments with potentially moving obstacles, where a large number of agents are required to maintain safety using only local information and reach their goals. This paper addresses the problem of collision avoidance, scalability, and generalizability by introducing graph control barrier functions (GCBFs) for distributed control. The newly introduced GCBF is based on the well-established CBF theory for safety guarantees but utilizes a graph structure for scalable and generalizable decentralized control. We use graph neural networks to learn both neural a GCBF certificate and distributed control. We also extend the framework from handling state-based models to directly taking point clouds from LiDAR for more practical robotics settings. We demonstrated the efficacy of GCBF in a variety of numerical experiments, where the number, density, and traveling distance of agents, as well as the number of unseen and uncontrolled obstacles increase. Empirical results show that GCBF outperforms leading methods such as MAPPO and multi-agent distributed CBF (MDCBF). Trained with only 16 agents, GCBF can achieve up to 3 times improvement of success rate (agents reach goals and never encountered in any collisions) on < 500 agents, and still maintain more than 50% success rates for > 1000 agents when other methods completely fail.
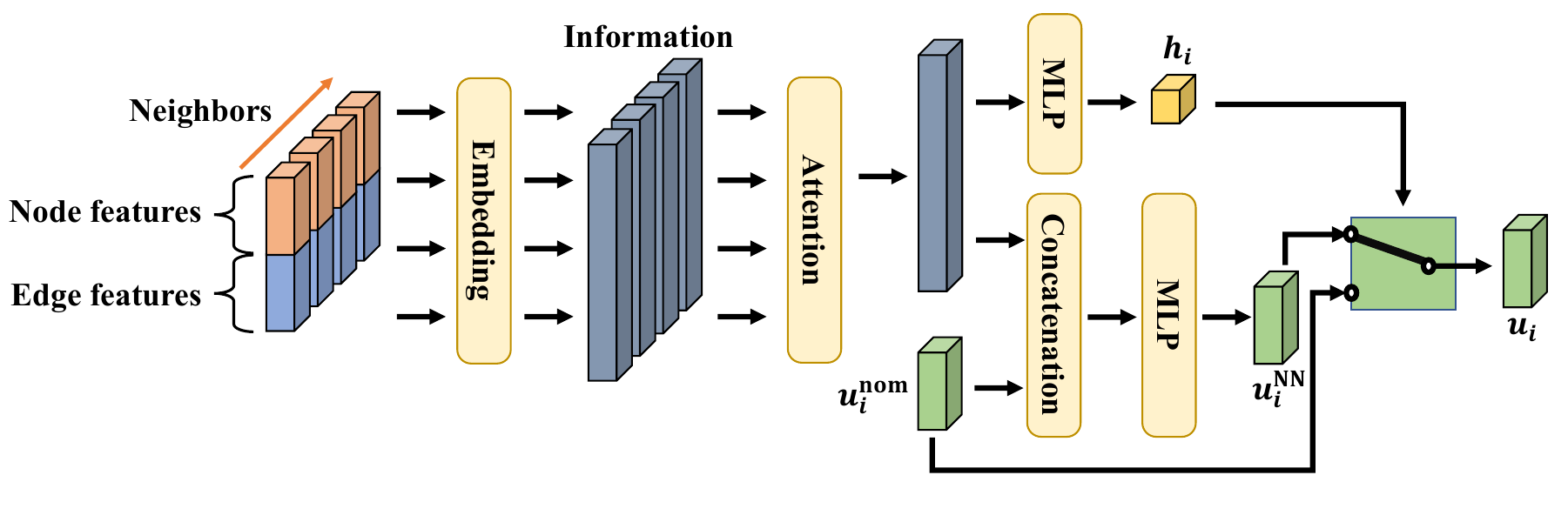
We design the node features to be the indicators of the types of the nodes (agent/LiDAR hitting point/goal), and edge features to be the relative positions, velocities, etc. The information is processed by the graph neural network with attention, which outputs the CBF value \(h_i\) and the collision-avoidance control \(u_i^\mathrm{NN}\). The learned CBF determines whether to use the nominal controller \(u_i^\mathrm{nom}\) or switch to the collision-avoidance controller \(u_i^\mathrm{NN}\).
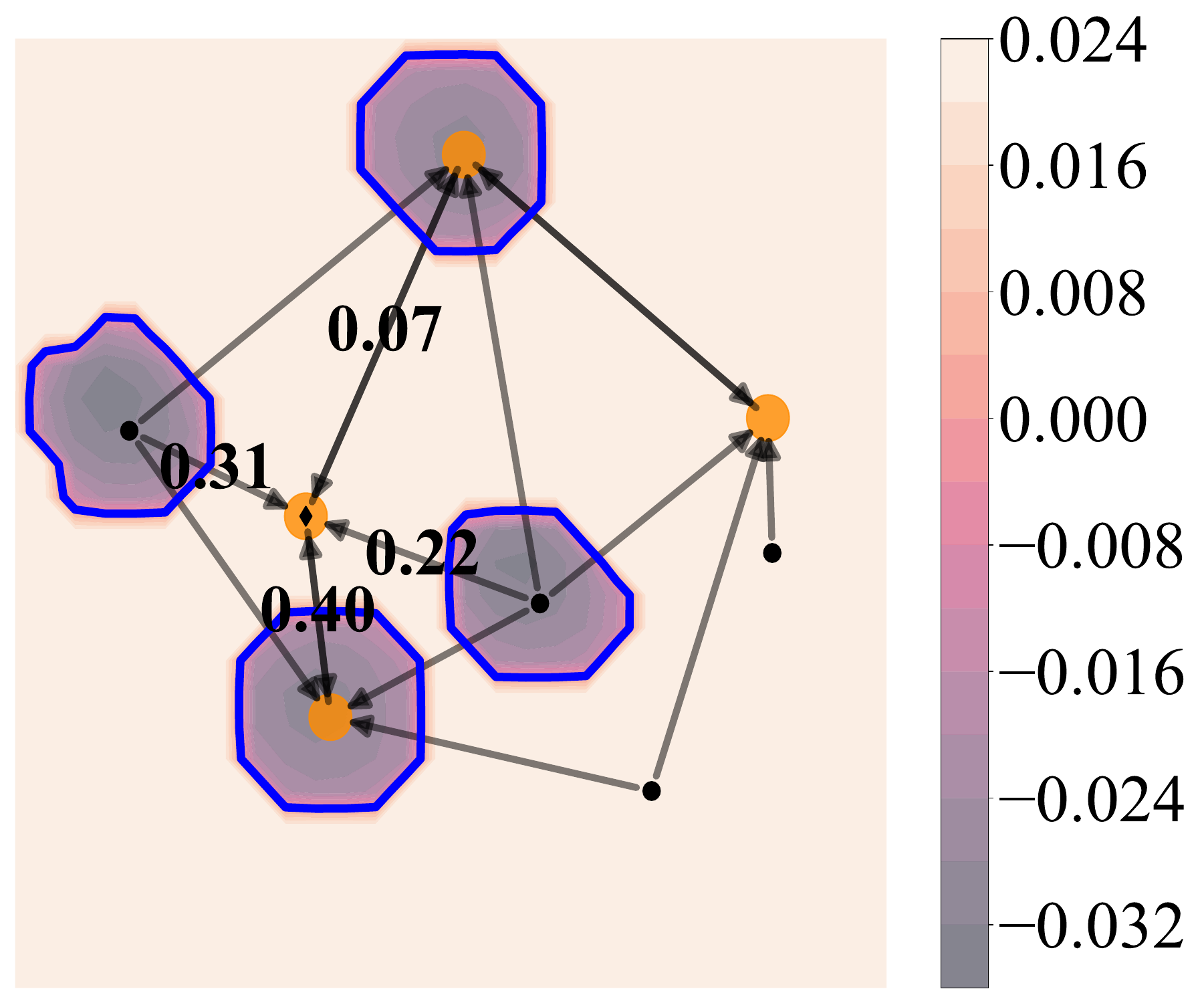
The learned CBF contour with the attention value.
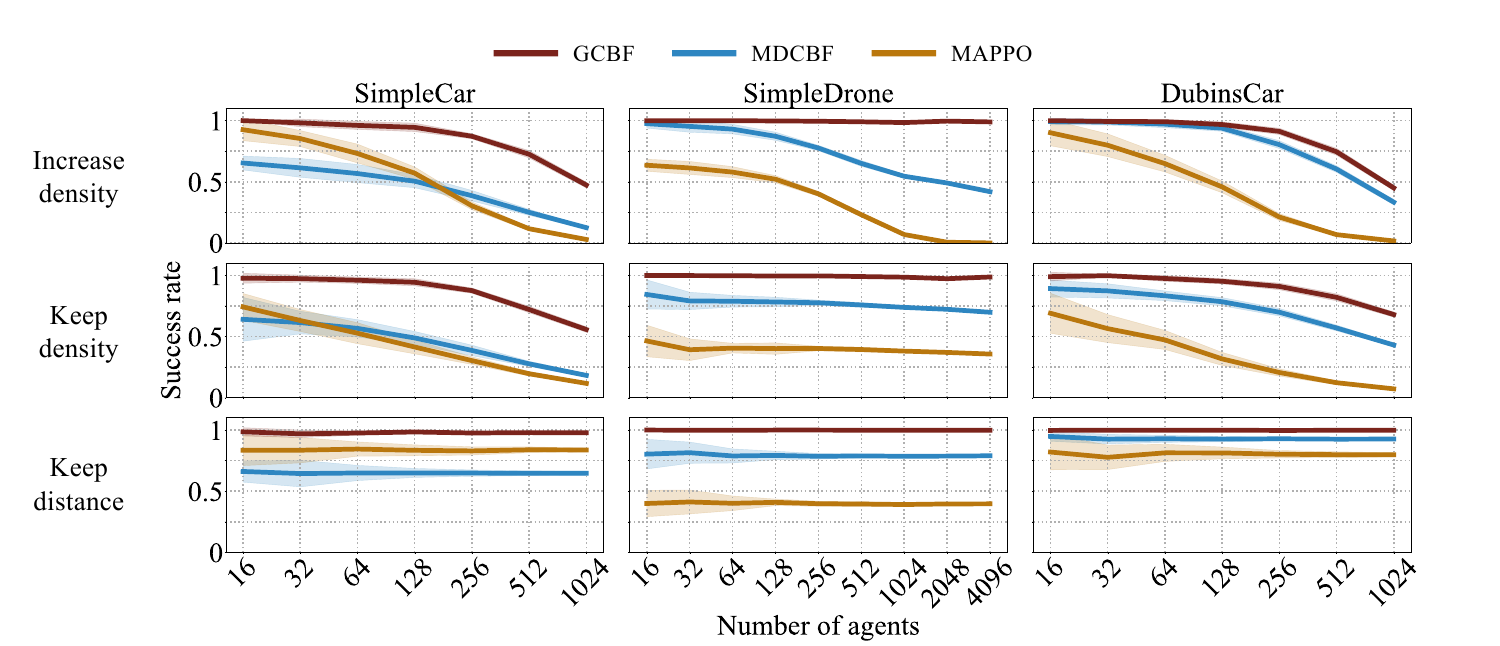
GCBF outperforms the baselines across the three environments and the three sets of experiments, namely, increasing density of the agents in a fixed workspace, increasing the size of the workspace to keep the density same, and increasing the size of the workspace but limiting the average distance traveled by agents. GCBF outperforms them because of a better structure than MDCBF, and RL sacrifies safety.
This work is the fundation of our work GCBF+. For a survey of the field of learning safe control for multi-robot systems, see this paper.
@inproceedings{zhang2023gcbf,
title={Neural graph control barrier functions guided distributed collision-avoidance multi-agent control},
author={Zhang, Songyuan and Garg, Kunal and Fan, Chuchu},
booktitle={Conference on Robot Learning},
pages={2373--2392},
year={2023},
organization={PMLR}
}