Better results than RL
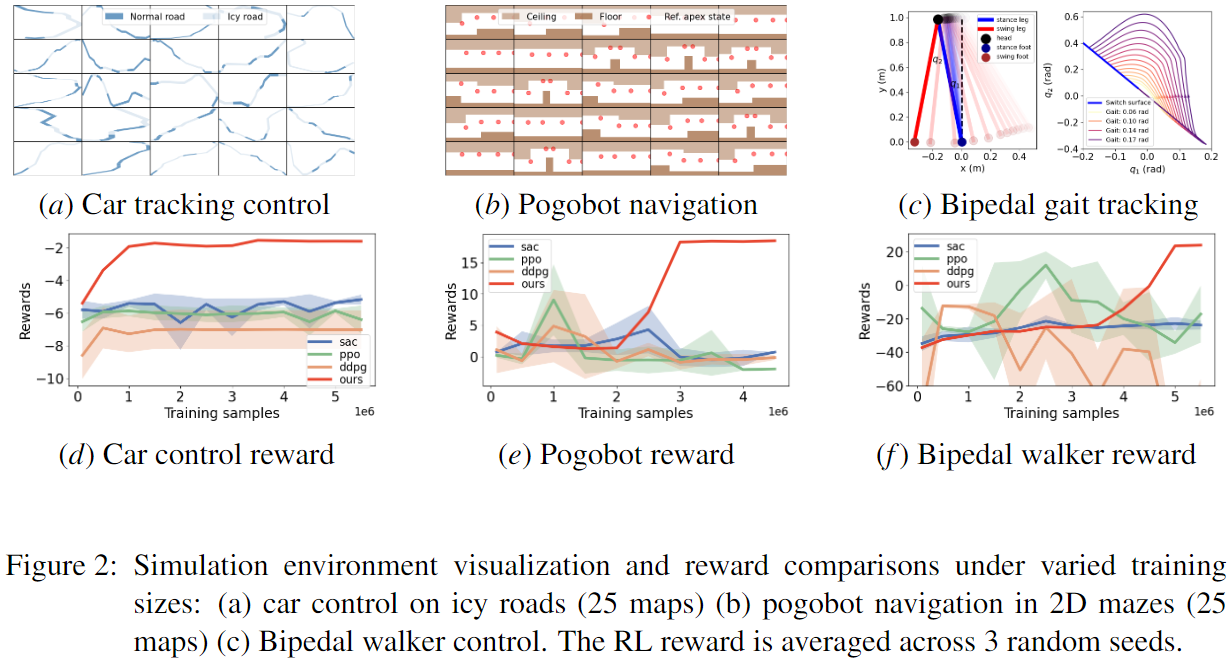
Hybrid systems are prevalent in robotics. However, ensuring the stability of hybrid systems is challenging due to sophisticated continuous and discrete dynamics. A system with all its subsystems stable can still be unstable. Hence special treatments are required at mode switchings to stabilize the system. In this work, we propose a hierarchical, neural network (NN)-based method to control general hybrid systems. For each subsystem mode, we first learn an NN Lyapunov function and an NN controller to ensure the states within the region of attraction (RoA) can be stabilized. Then an RoA NN estimator is learned across different modes. Upon mode switching, we propose a differentiable planner to ensure the states after switching can land in next mode's RoA, hence stabilizing the hybrid system. We provide novel theoretical stability guarantees and conduct experiments in car tracking control, pogobot navigation, and bipedal walker locomotion. Our method only requires 0.25X of the training time as needed by other learning-based methods. With low running time (10~50X faster than model predictive control (MPC)), our controller achieves a higher stability/success rate over other baselines such as MPC, reinforcement learning (RL), common Lyapunov methods (CLF), linear quadratic regulator (LQR), quadratic programming (QP) and Hamilton-Jacobian-based methods (HJB).